| There is a dramatic video on youtube, from “Alpine Savvy,”
showing how to saw through a 9mm climbing rope, with a thin 2mm nylon cord
pulled back and forth quickly. The
operative words are “back and forth,” “thin,” and especially, “quickly.” It
is notable that the Alpine Savvy site also says it is OK to rap one time on just
webbing, without a metal rap ring or quicklink… but NOT to top rope, since that
implies possible quick motion of the rope pulling over the webbing, under a
substantial force. Below are videos of several tests of ropes running across slings or ropes under load, perhaps with surprising results. The middle and right-most video take 13s to cycle through each word slide, so be patient! |
||||
| |
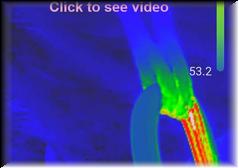 8mm nylon rope under load pulled one-way through two spliced eyes in 4mm Dyneema sling |
 Back-and-forth test with 8mm PET rope on nylon webbing. Allow 13 seconds between slides |
 Back-and-forth test with 6mm PET rope on 2x6mm PET rope and 6mm Dyneeema on 2x6mm Dyneema. Allow 13 seconds between slides | |
|
Above at left is an infrared video of an 8mm nylon rope, going one direction (left to right) at about 40 cm/sec and 0.31 kN (~70 lbs) normal force, through a sling of bare 4mm (18 kN) Dyneema. This was the 8th time I had done this test on the same sling, repeating the setup as fast as I could. Temps are in F. I had a harness on my waist attached to a load cell and then to one end of the rope; I gripped the other strand of the rope in my gloved left hand, and pushed backward as hard as I could for 14m. (The photography was done with a black background, under a black shroud.) Simply put, the Dyneema never got anywhere near hot enough to melt. The relevance might be for an extremely unusual situation, where you are trying to pull a rope after a rap, and the rope is somewhat stuck, so it pulls through the sling gradually under a fraction of your body weight. |
||||
|
The middle and right-most videos above test situations where the moving rope is going two directions, back-and-forth,
over the statoinary "slings." The amount of moving rope that contacts
the slings is ~1 m -- the same 1 m over and over. In the middle video,
the "sling" is 1" climspec tubular webbing; in the rightmost video, the
"sling" is two strands of the same rope as the moving rope.
The heat generated by surface friction in the rope-sling system per unit time is roughly proportional to
There is no simple way to predict how this heat will be partitioned between the rope and the sling. In the right-most video, the heat in the "sling" will be largely restricted to the small 2*diameter*diameter area shown in the 5th slide, with some side-blurring controlled by slow diffusion. In the moving rope, the surface-friction-generated heat will be distributed all along the moving section (about 1 m), with a concentration toward the center, where the rope moves more slowly and changes direction.
The moving rope itself, but not the sling, also heats up from internal friction, because the internal fibers rub on each other as the rope bends; this heat also increases with time at a rate approximately proportional to the average speed of movement—and this heat is also over the entire length of moving rope, with a concentration toward the center. It is generated throughout the diameter of rope that gets bent over the sling, not just at the surface. Similarly, the heat production with time inside the moving rope is
(Speed of moving rope)* (normal force, which is some fraction of my body weight)*(internal coefficient of friction of moving rope)
The moving rope never breaks in the above two-way tests, but by increasing in temperature, it contributes to the temperature rise melting of the sling it contacts. By contrast, in the one-way rope system, the heat generated in the rope is simply carried away from the sling, forever.
The loss of heat from the rope-sling system is mainly from conduction to the air and subsequent convective flow. There is some radiative loss, but it tends to go as absolute temperature to the 4th power, and is just a minor component at lower temperatures. Newtons' empirical law of cooling tells us that the rate of heat loss is proportional to the difference in temperature between the rope and its surroundings—so the hotter the rope gets, the faster it will lose heat. There is also conduction along the axis of the rope, so the heat has to raise the temperature of more and more rope as time goes on—but with fast enough rope movement, most of the heat is concentrated, the spreading of the heat is relatively unimportant. If the rope moves fast enough, it overcomes the conductive-convective losses, and temperature builds up locally to the melting point of the rope. (Latent heat of melting is rather small.)
|
||||